三角関数とは

三角関数 (英：trigonometric function) とは、三角法において角の大きさと線分の長さの関係を表す関数のこと。

三角関数の性質

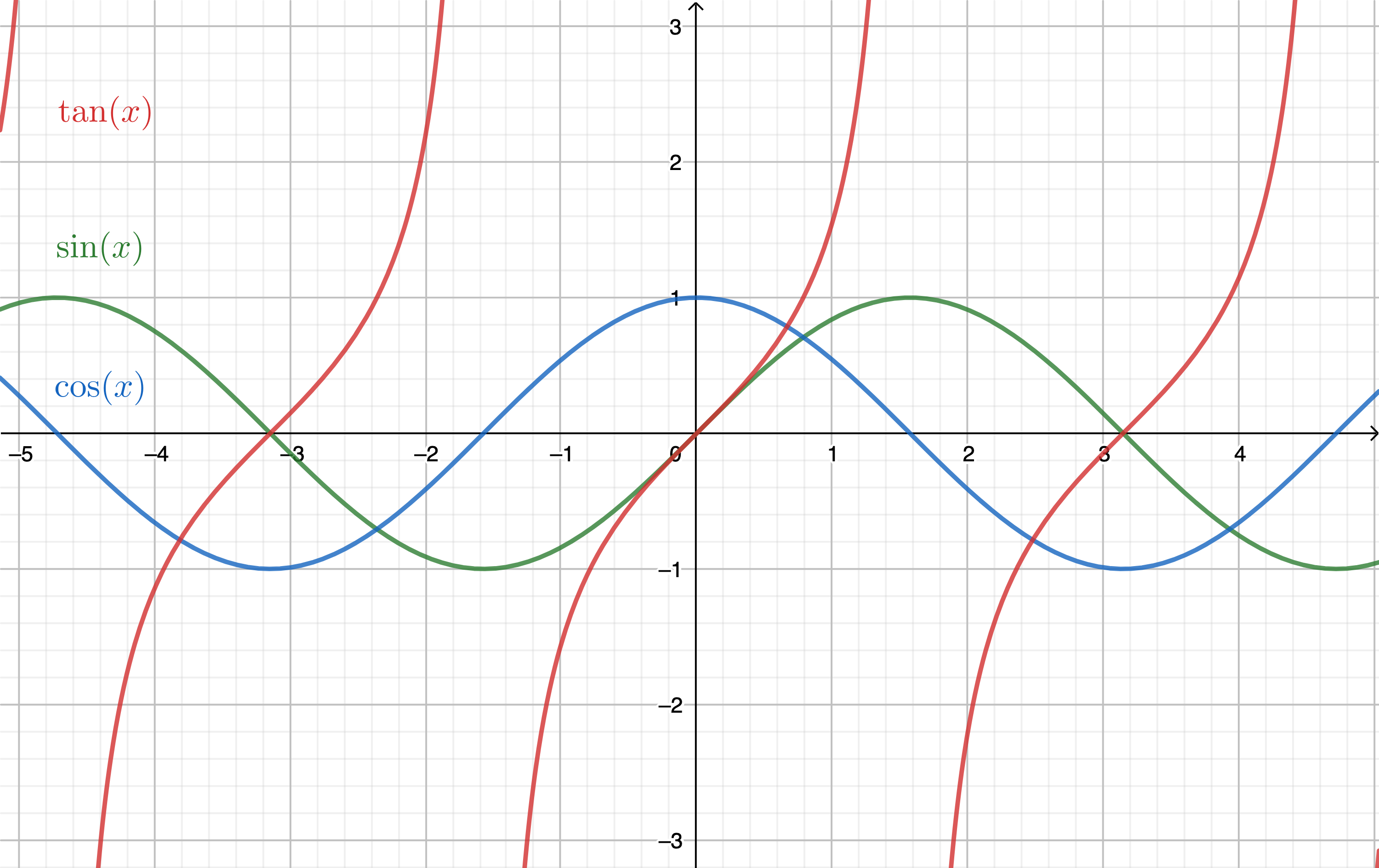
周期性

+ 90°	+ 180°	+ 270°	+ 360°
$\displaystyle \sin\left(\theta+\frac{1}{2}\pi\right) = +\cos\theta$	$\sin(\theta+\pi) = -\sin\theta$	$\displaystyle \sin\left(\theta+\frac{3}{2}\pi\right) = -\cos\theta$	$\sin(\theta+2\pi) = +\sin\theta$
$\displaystyle \cos\left(\theta+\frac{1}{2}\pi\right) = -\sin\theta$	$\cos(\theta+\pi) = -\cos\theta$	$\displaystyle \cos\left(\theta+\frac{3}{2}\pi\right) = +\sin\theta$	$\cos(\theta+2\pi) = +\cos\theta$
$\displaystyle \tan\left(\theta+\frac{1}{2}\pi\right) = -\frac{\cos\theta}{\sin\theta}$	$\tan(\theta+\pi) = \tan\theta$	$\displaystyle \tan\left(\theta+\frac{3}{2}\pi\right) = -\frac{\cos\theta}{\sin\theta}$	$\tan(\theta+2\pi) = \tan\theta$

還元公式

負角：

$\begin{aligned} \sin(-\theta) &= -\sin\theta \cr \cos(-\theta) &= \cos\theta \cr \tan(-\theta) &= -\tan\theta \end{aligned}$

余角：

$\begin{aligned} \sin\left(\frac{\pi}{2}-\theta\right) &= \cos\theta \cr \cos\left(\frac{\pi}{2}-\theta\right) &= \sin\theta \cr \tan\left(\frac{\pi}{2}-\theta\right) &= \frac{1}{\tan\theta} \end{aligned}$

補角：

$\begin{aligned} \sin(\pi-\theta) &= \sin\theta \cr \cos(\pi-\theta) &= -\cos\theta \cr \tan(\pi-\theta) &= -\tan\theta \end{aligned}$

変換公式

	$\sin\theta$	$\cos\theta$	$\tan\theta$
$\sin\theta=$	-	$\pm\sqrt{1-\cos^2\theta}$	$\displaystyle \pm\frac{\tan\theta}{\sqrt{1+\tan^2\theta}}$
$\cos\theta=$	$\pm\sqrt{1-\sin^2\theta}$	-	$\displaystyle \pm\frac{1}{\sqrt{1+\tan^2\theta}}$
$\tan\theta=$	$\displaystyle \pm\frac{\sin\theta}{\sqrt{1-\sin^2\theta}}$	$\displaystyle \pm\frac{\sqrt{1-\cos^2\theta}}{\cos\theta}$	-

各変換公式の導出：

$\sin\theta=\pm\sqrt{1-\cos^2\theta}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \sin^2\theta &= 1 - \cos^2\theta \cr \cr \therefore \sin\theta &= \pm\sqrt{1-\cos^2\theta} \end{aligned}$

$\displaystyle \sin\theta = \pm\frac{\tan\theta}{\sqrt{1+\tan^2\theta}}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \frac{\sin^2\theta}{\tan^2\theta} + \sin^2\theta &= 1 \cr \sin^2\theta &= \frac{\tan^2\theta}{1+\tan^2\theta} \cr \cr \therefore \sin\theta &= \pm\frac{\tan\theta}{\sqrt{1+\tan^2\theta}} \end{aligned}$

$\cos\theta = \pm\sqrt{1-\sin^2\theta}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \cos^2\theta &= 1-\sin^2\theta \cr \cr \therefore \cos\theta &= \pm\sqrt{1-\sin^2\theta} \end{aligned}$

$\displaystyle \cos\theta = \pm\frac{1}{\sqrt{1+\tan^2\theta}}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \cos^2\theta + \cos^2\theta\tan^2\theta &= 1 \cr \cos^2\theta &= \frac{1}{1+\tan^2\theta} \cr \cr \therefore \cos\theta &= \pm\frac{1}{\sqrt{1+\tan^2\theta}} \end{aligned}$

$\displaystyle \tan\theta = \pm\frac{\sin\theta}{\sqrt{1-\sin^2\theta}}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \frac{\sin^2\theta}{\tan^2\theta} + \sin^2\theta &= 1 \cr \tan^2\theta &= \frac{\sin^2\theta}{1-\sin^2\theta} \cr \cr \therefore \tan\theta &= \pm\frac{\sin\theta}{\sqrt{1-\sin^2\theta}} \end{aligned}$

$\displaystyle \tan\theta = \pm\frac{\sqrt{1-\cos^2\theta}}{\cos\theta}$ ：

$\begin{aligned} \cos^2\theta + \sin^2\theta &= 1 \cr \cos^2\theta + \cos^2\theta\tan^2\theta &= 1 \cr \tan^2\theta &= \frac{1-\cos^2\theta}{\cos^2\theta} \cr \cr \therefore \tan\theta &= \pm\frac{\sqrt{1-\cos^2\theta}}{\cos\theta} \end{aligned}$

三角関数の加法定理

$\begin{aligned} \text{余弦関数の加法定理} &: \cos(\alpha\pm\beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \vphantom{\int} \\ \text{正弦関数の加法定理} &: \sin(\alpha\pm\beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta \vphantom{\int} \\ \text{正接関数の加法定理} &: \tan(\alpha\pm\beta) = \frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta} \\ \end{aligned}$

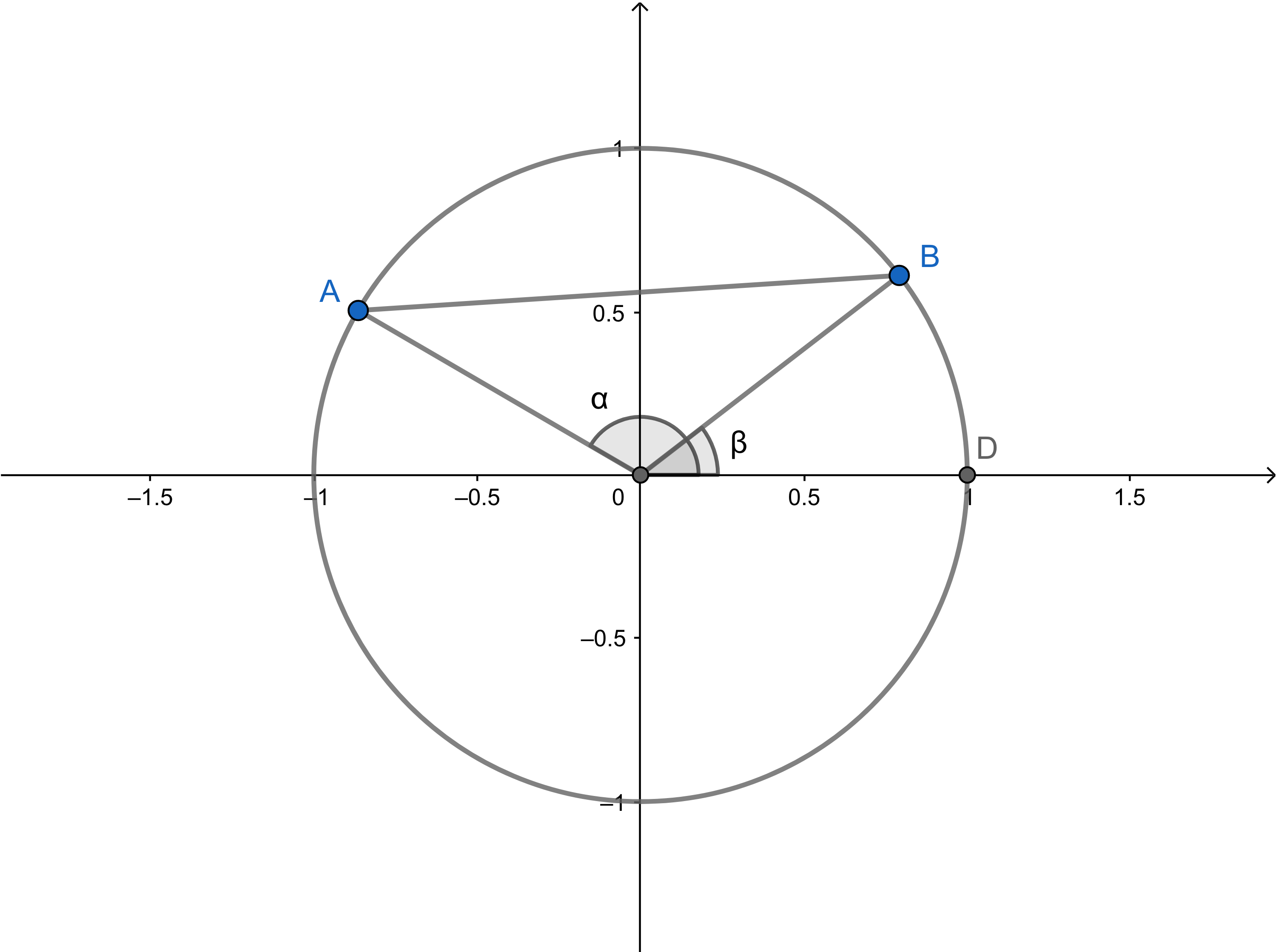
余弦の加法定理の証明：

余弦定理により、

$\begin{aligned} {AB}^2 &= 1^2 + 1^2 - 2\cdot 1\cdot 1\cdot\cos(\alpha-\beta) \cr &= 2 - 2\cos(\alpha-\beta) \end{aligned}$

ピタゴラスの定理により、

$\begin{aligned} AB^2 &= (\cos\alpha-\cos\beta)^2 + (\sin\alpha-\sin\beta)^2 \cr &= \cos^2\alpha+\cos^2\beta - 2\cos\alpha\cos\beta + \sin^2\alpha + \sin^2\beta - 2\sin\alpha\sin\beta \cr &= (\cos^2\alpha+\sin^2\alpha) + (\cos^2\beta+\sin^2\beta) - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta \cr &= 2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta \end{aligned}$

$AB^2$ を共に求めていることから、

$2 - 2\cos(\alpha-\beta) = 2 - 2\cos\alpha\cos\beta - 2\sin\alpha\sin\beta$

$\cos(\alpha-\beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta \tag{1}$

$(1)$ の $\beta$ を $-\beta^\prime$ とすると、

$\begin{aligned} \cos(\alpha-(-\beta^\prime)) &= \cos\alpha\cos(-\beta^\prime)+ \sin\alpha\sin(-\beta^\prime) \end{aligned}$

$\cos(\alpha+\beta^\prime) = \cos\alpha\cos\beta^\prime - \sin\alpha\sin\beta^\prime \tag{2}$

$(1),(2)$ により、

$\therefore \cos(\alpha\pm\beta) = \cos\alpha\cos\beta \mp \sin\alpha\sin\beta$

正弦の加法定理の証明：

余弦の加法定理の $\beta$ を $\displaystyle \beta^\prime+\frac{1}{2}\pi$ とすると、

$\begin{aligned} \cos\left[\alpha-\left(\beta^\prime+\frac{1}{2}\pi\right)\right] &= \cos\alpha\cos\left(\beta^\prime+\frac{1}{2}\pi\right) + \sin\alpha\sin\left(\beta^\prime+\frac{1}{2}\pi\right) \cr \cos\left[(\alpha-\beta^\prime)-\frac{1}{2}\pi\right] &= \cos\alpha\cos\left(\beta^\prime+\frac{1}{2}\pi\right) + \sin\alpha\sin\left(\beta^\prime+\frac{1}{2}\pi\right) \cr \sin(\alpha-\beta^\prime) &= \cos\alpha(-\sin\beta^\prime) + \sin\alpha\cos\beta^\prime \end{aligned}$

$\sin(\alpha-\beta^\prime) = \sin\alpha\cos\beta^\prime - \cos\alpha\sin\beta^\prime \tag{1}$

$(1)$ の $\beta^\prime$ を $-\beta^{\prime\prime}$ とすると、 $\sin(\alpha-(-\beta^{\prime\prime})) = \sin\alpha\cos(-\beta^{\prime\prime}) - \cos\alpha\sin(-\beta^{\prime\prime})$

$\sin(\alpha+\beta^{\prime\prime}) = \sin\alpha\cos(\beta^{\prime\prime}) + \cos\alpha\sin\beta^{\prime\prime} \tag{2}$

$(1),(2)$ により、

$\therefore \sin(\alpha\pm\beta) = \sin\alpha\cos\beta \pm \cos\alpha\sin\beta$

正接の加法定理の証明：

余弦の加法定理と正弦の加法定理により、

$\begin{aligned} \tan(\alpha+\beta) &= \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \cr &= \frac{\sin\alpha\cos\beta + \cos\alpha\sin\beta}{\cos\alpha\cos\beta - \sin\alpha\sin\beta} \cr &= \frac{\sin\alpha/\cos\alpha+\sin\beta/\cos\beta}{1-\sin\alpha\sin\beta/\cos\alpha\cos\beta} \end{aligned}$

$\tan(\alpha+\beta) = \frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta} \tag{1}$

$(1)$ の $\beta$ を $-\beta^\prime$ とすると、

$\tan[\alpha+(-\beta^\prime)] = \frac{\tan\alpha+\tan(-\beta^\prime)}{1-\tan\alpha\tan(-\beta^\prime)}$

$\tan(\alpha-\beta^\prime) = \frac{\tan\alpha-\tan\beta^\prime}{1+\tan\alpha\tan\beta^\prime} \tag{2}$

$(1),(2)$ により、

$\therefore \tan(\alpha\pm\beta) = \frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}$

三角関数の積和の公式

$\begin{aligned} \text{余弦関数と正弦関数の積} &: \cos\alpha\sin\beta = \frac{1}{2}\left(\sin(\alpha+\beta)-\sin(\alpha-\beta)\right) \\ &: \sin\alpha\cos\beta = \frac{1}{2}\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right) \\ \text{余弦関数同士の積} &: \cos\alpha\cos\beta = \frac{1}{2}\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right) \\ \text{正弦関数同士の積} &: \sin\alpha\sin\beta = -\frac{1}{2}\left(\cos(\alpha+\beta)-\cos(\alpha-\beta)\right) \\ \end{aligned}$

余弦関数と正弦関数の積：

三角関数の加法定理より、

$\begin{aligned} \sin(\alpha\pm\beta) &= \sin\alpha\cos\beta \pm \cos\alpha\sin\beta \cr \sin(\alpha+\beta) + \sin(\alpha-\beta) &= (\sin\alpha\cos\beta + \cos\alpha\sin\beta) + (\sin\alpha\cos\beta - \cos\alpha\sin\beta) \cr &= 2\sin\alpha\cos\beta \cr \sin(\alpha+\beta) - \sin(\alpha-\beta) &= (\sin\alpha\cos\beta + \cos\alpha\sin\beta) - (\sin\alpha\cos\beta - \cos\alpha\sin\beta) \cr &= 2\cos\alpha\sin\beta \cr \cr \therefore \frac{}{}\sin\alpha\cos\beta &= \frac{1}{2}\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right) \cr \cos\alpha\sin\beta &= \frac{1}{2}\left(\sin(\alpha+\beta)-\sin(\alpha-\beta)\right) \end{aligned}$

余弦関数同士の積：

三角関数の加法定理より、

$\begin{aligned} \cos(\alpha\pm\beta) &= \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \cr \cos(\alpha+\beta) + \cos(\alpha-\beta) &= (\cos\alpha\cos\beta - \sin\alpha\sin\beta ) + (\cos\alpha\cos\beta + \sin\alpha\sin\beta ) \cr &= 2\cos\alpha\cos\beta \cr \cr \therefore \cos\alpha\cos\beta &= \frac{1}{2}\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right) \end{aligned}$

正弦関数同士の積：

三角関数の加法定理より、

$\begin{aligned} \cos(\alpha\pm\beta) &= \cos\alpha\cos\beta \mp \sin\alpha\sin\beta \cr \cos(\alpha+\beta) - \cos(\alpha-\beta) &= (\cos\alpha\cos\beta - \sin\alpha\sin\beta ) - (\cos\alpha\cos\beta + \sin\alpha\sin\beta ) \cr &= -2\sin\alpha\sin\beta \cr \cr \therefore \sin\alpha\sin\beta &= -\frac{1}{2}\left(\cos(\alpha+\beta)-\cos(\alpha-\beta)\right) \end{aligned}$

三角関数の和積の公式

$\begin{aligned} \text{余弦関数同士の和} &: \cos x +\cos y = 2\cos\frac{x+y}{2}\cos\frac{x-y}{2} \\ \text{余弦関数同士の差} &: \cos x-\cos y = -2\sin\frac{x+y}{2}\sin\frac{x-y}{2} \\ \text{正弦関数同士の和} &: \sin x + \sin y = 2\sin\frac{x+y}{2}\cos\frac{x-y}{2} \\ \text{正弦関数同士の差} &: \sin x - \sin y = 2\cos\frac{x+y}{2}\sin\frac{x-y}{2} \\ \end{aligned}$

余弦関数同士の和の導出：

積和の公式から、

$\cos\alpha\cos\beta = \frac{1}{2}\left(\cos(\alpha+\beta)+\cos(\alpha-\beta)\right) \tag{1}$

$x=\alpha+\beta, ~y=\alpha-\beta$ とすると、

$\begin{aligned} x + y &= (\alpha+\beta) + (\alpha-\beta) \cr \alpha &= \frac{x+y}{2} \cr x - y &= (\alpha+\beta) - (\alpha-\beta) \cr \beta &= \frac{x-y}{2} \end{aligned} \tag{2}$

$(2)$ を $(1)$ に代入すると、

$\begin{aligned} \cos\frac{x+y}{2}\cos\frac{x-y}{2} &= \frac{1}{2}(\cos x+\cos y) \cr \cr \therefore \cos x+\cos y &= 2\cos\frac{x+y}{2}\cos\frac{x-y}{2} \end{aligned}$

余弦関数同士の差の導出：

積和の公式から、

$\sin\alpha\sin\beta = -\frac{1}{2}\left(\cos(\alpha+\beta)-\cos(\alpha-\beta)\right) \tag{1}$

$x=\alpha+\beta, ~y=\alpha-\beta$ とすると、

$\begin{aligned} x + y &= (\alpha+\beta) + (\alpha-\beta) \cr \alpha &= \frac{x+y}{2} \cr x - y &= (\alpha+\beta) - (\alpha-\beta) \cr \beta &= \frac{x-y}{2} \end{aligned} \tag{2}$

$(2)$ を $(1)$ に代入すると、

$\begin{aligned} \sin\frac{x+y}{2}\sin\frac{x-y}{2} &= -\frac{1}{2}(\cos x-\cos y) \cr \cr \therefore \cos x-\cos y &= -2\sin\frac{x+y}{2}\sin\frac{x-y}{2} \end{aligned}$

正弦関数同士の和の導出：

積和の公式から、

$\sin\alpha\cos\beta = \frac{1}{2}\left(\sin(\alpha+\beta)+\sin(\alpha-\beta)\right) \tag{1}$

$x=\alpha+\beta, ~y=\alpha-\beta$ とすると、

$\begin{aligned} x + y &= (\alpha+\beta) + (\alpha-\beta) \cr \alpha &= \frac{x+y}{2} \cr x - y &= (\alpha+\beta) - (\alpha-\beta) \cr \beta &= \frac{x-y}{2} \end{aligned} \tag{2}$

$(2)$ を $(1)$ に代入すると、

$\begin{aligned} \sin\frac{x+y}{2}\cos\frac{x-y}{2} &= \frac{1}{2}\left(\sin x +\sin y\right) \cr \cr \therefore \sin x + \sin y &= 2\sin\frac{x+y}{2}\cos\frac{x-y}{2} \end{aligned}$

正弦関数同士の差の導出：

積和の公式から、

$\cos\alpha\sin\beta = \frac{1}{2}\left(\sin(\alpha+\beta)-\sin(\alpha-\beta)\right) \tag{1}$

$x=\alpha+\beta, ~y=\alpha-\beta$ とすると、

$\begin{aligned} x + y &= (\alpha+\beta) + (\alpha-\beta) \cr \alpha &= \frac{x+y}{2} \cr x - y &= (\alpha+\beta) - (\alpha-\beta) \cr \beta &= \frac{x-y}{2} \end{aligned} \tag{2}$

$(2)$ を $(1)$ に代入すると、

$\begin{aligned} \cos\frac{x+y}{2}\sin\frac{x-y}{2} &= \frac{1}{2}\left(\sin x -\sin y\right) \cr \cr \therefore \sin x - \sin y &= 2\cos\frac{x+y}{2}\sin\frac{x-y}{2} \end{aligned}$

三角関数の微分

$\begin{aligned} \text{余弦関数の微分} &: (\cos x)^\prime = -\sin x \vphantom{\int} \\ \text{正弦関数の微分} &: (\sin x)^\prime = \cos x \vphantom{\int} \\ \text{正接関数の微分} &: (\tan x)^\prime = \frac{1}{\cos^2 x} \end{aligned}$

余弦関数の微分の導出： $\begin{aligned} (\cos x)^\prime &= \lim_{h\to 0}\frac{\cos(x+h)-\cos x}{h} \\ &= \lim_{h\to 0}\frac{\cos x\cos h - \sin x\sin h - \cos x}{h} \\ &= \lim_{h\to 0}\left[\frac{\cos x(\cos h - 1)}{h} - \sin x\frac{\sin h}{h}\right] \\ &= -\sin x \vphantom{\int} \\ \\ \therefore (\cos x)^\prime &= -\sin x \end{aligned}$

正弦関数の微分の導出： $\begin{aligned} (\sin x)^\prime &= \lim_{h\to 0}\frac{\sin(x+h)-\sin x}{h} \\ &= \lim_{h\to 0}\frac{\sin x\cos h + \cos x\sin h - \sin x}{h} \\ &= \lim_{h\to 0}\left[\frac{\sin x (\cos h-1)}{h} + \cos x\frac{\sin h}{h}\right] \\ &= \cos x \vphantom{\int} \\ \cr \therefore (\sin x)^\prime &= \cos x \end{aligned}$

正接関数の微分の導出： $\begin{aligned} (\tan x)^\prime &= \left(\frac{\sin x}{\cos x}\right)^\prime \cr &= \frac{(\sin x)^\prime\cos x - \sin x(\cos x)^\prime}{\cos^2 x} \quad \because \text{商の微分法則} \cr &= \frac{\cos^2x + \sin^2 x}{\cos^2 x} \because (\sin x)^\prime = \cos x, ~(\cos x)^\prime = -\sin x \cr &= \frac{1}{\cos^2 x} \cr \cr \therefore (\tan x)^\prime &= \frac{1}{\cos^2 x} \end{aligned}$

三角関数の積分

$\begin{aligned} \text{余弦関数の不定積分} &: \int{\cos x~dx} = \sin x + C \\ \text{正弦関数の不定積分} &: \int{\sin x}~dx = -\cos x + C \\ \text{正接関数の不定積分} &: \int{\tan x}~dx = -\ln|\cos x| + C \\ \end{aligned}$

余弦関数の不定積分の導出：

$\begin{aligned} \int{\cos x}~dx &= \int(\sin x)^\prime~dx \\ &= \sin x + C \\ \\ \therefore \int{\cos x}~dx &= \sin x + C \end{aligned}$

正弦関数の不定積分の導出：

$\begin{aligned} \int{\sin x}~dx &= \int(-\cos x)^\prime~dx\\ &= -\cos x + C \\ \\ \therefore \int{\sin x}~dx &= -\cos x + C \end{aligned}$

正接関数の不定積分の導出：

$\begin{aligned} \int{\tan x}~dx &= \int{\frac{\sin x}{\cos x}~dx} \cr &= \int{-\frac{(\cos x)^\prime}{\cos x}}~dx \cr &= -\ln|\cos x| + C \cr \cr \therefore \int{\tan x}~dx &= -\ln|\cos x| + C \end{aligned}$

三角関数の直交性

$\begin{aligned}\text{余弦関数同士の積の積分}&: \int_0^{2\pi}\cos(mt)\cos(nt)~dt = \pi\delta_{m,n} \quad (m,n\in\N_{\ge 0}) \\\text{正弦関数同士の積の積分}&: \int_0^{2\pi}\sin(mt)\sin(nt)~dt = \pi\delta_{m,n} \quad (m,n\in\N_{\ge 0}) \\\text{余弦関数と正弦関数の積の積分}&: \int_0^{2\pi}\cos(mt)\sin(nt)~dt = 0 \quad (m,n\in\N_{\ge 0})\end{aligned}$

余弦関数同士の積の積分：

$\begin{aligned}\int_0^{2\pi}\cos(mt)\cos(nt)~dt&= \frac{1}{2}\int_0^{2\pi}\cos\big((m+n)t\big)+\cos\big((m-n)t\big)~dt \quad \because \text{三角関数の積和公式} \\&= \begin{cases}\displaystyle \frac{1}{2}\int_0^{2\pi}\cos\big((m+n)t\big)+\cos\big((m-n)t\big)~dt & \text{if }m\ne n \\\displaystyle \frac{1}{2}\int_0^{2\pi}\cos(2mt)+1~dt & \text{if }m=n \\\end{cases} \\&= \begin{cases}\displaystyle \frac{1}{2}\left[\frac{\sin\big((m+n)t\big)}{m+n}+\frac{\sin\big((m-n)t\big)}{m-n}\right]_0^{2\pi} & \text{if }m\ne n \\\displaystyle \frac{1}{2}\left[\frac{\sin\big(2mt\big)}{2m}+t\right]_0^{2\pi} & \text{if }m=n \\\end{cases} \\&= \begin{cases}0 & \text{if }m\ne n \vphantom{\displaystyle\int} \\\pi & \text{if }m=n \vphantom{\displaystyle\int} \\\end{cases} \\\\\therefore \int_0^{2\pi}\cos(mt)\cos(nt)~dt&= \pi\delta_{m,n} \quad (m,n\in\N_{\ge 0})\end{aligned}$

正弦関数同士の積の積分：

$\begin{aligned}\int_0^{2\pi}\sin(mt)\sin(nt)~dt&= -\frac{1}{2}\int_0^{2\pi}\cos\big((m+n)t\big)-\cos\big((m-n)t\big)~dt \quad \because \text{三角関数の積和公式} \\&= \begin{cases}\displaystyle -\frac{1}{2}\int_0^{2\pi}\cos\big((m+n)t\big)-\cos\big((m-n)t\big)~dt & \text{if }m\ne n \\\displaystyle -\frac{1}{2}\int_0^{2\pi}\cos(2mt)-1~dt & \text{if }m=n \\\end{cases} \\&= \begin{cases}\displaystyle -\frac{1}{2}\left[\frac{\sin\big((m+n)t\big)}{m+n}-\frac{\sin\big((m-n)t\big)}{m-n}\right]_0^{2\pi} & \text{if }m\ne n \\\displaystyle -\frac{1}{2}\left[\frac{\sin\big(2mt\big)}{2m}-t\right]_0^{2\pi} & \text{if }m=n \\\end{cases} \\&= \begin{cases}0 & \text{if }m\ne n \vphantom{\displaystyle\int} \\\pi & \text{if }m=n \vphantom{\displaystyle\int} \\\end{cases} \\\\\therefore \int_0^{2\pi}\sin(mt)\sin(nt)~dt&= \pi\delta_{m,n} \quad (m,n\in\N_{\ge 0})\end{aligned}$

余弦関数と正弦関数の積の積分：

$\begin{aligned}\int_0^{2\pi}\cos(mt)\sin(nt)~dt&= \frac{1}{2}\int_0^{2\pi}\sin\big((m+n)t\big)-\sin\big((m-n)t\big)~dt \quad \because \text{三角関数の積和公式} \\&= \begin{cases}\displaystyle \frac{1}{2}\int_0^{2\pi}\sin\big((m+n)t\big)-\sin\big((m-n)t\big)~dt & \text{if }m\ne n \\\displaystyle \frac{1}{2}\int_0^{2\pi}\sin(2mt)~dt & \text{if }m=n \\\end{cases} \\&= \begin{cases}\displaystyle \frac{1}{2}\left[-\frac{\cos\big((m+n)t\big)}{m+n}+\frac{\cos\big((m-n)t\big)}{m-n}\right]_0^{2\pi} & \text{if }m\ne n \\\displaystyle \frac{1}{2}\left[-\frac{\cos\big(2mt\big)}{2m}\right]_0^{2\pi} & \text{if }m=n \\\end{cases} \\&= \begin{cases}0 & \text{if }m\ne n \vphantom{\displaystyle\int} \\0 & \text{if }m=n \vphantom{\displaystyle\int} \\\end{cases} \\\\\therefore \int_0^{2\pi}\cos(mt)\sin(nt)~dt&= 0 \quad (m,n\in\N_{\ge 0})\end{aligned}$

三角関数のマクローリン展開

$\begin{aligned} \text{余弦関数のマクローリン展開} : \cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} +\cdots \\ &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k)!}x^{2k} \\ \text{正弦関数のマクローリン展開} : \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} +\cdots \\ &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)!}x^{2k+1} \\ \end{aligned}$

余弦関数のマクローリン展開の導出：

$\cos x$ をマクローリン展開すると、 $\begin{aligned} \cos x &= \sum_{k=0}^\infty\frac{\cos^{(k)}0}{k!}x^k \cr &= \frac{\cos^{(0)}0}{0!}x^0 + \frac{\cos^{(1)}0}{1!}x^1 + \frac{\cos^{(2)}0}{2!}x^2 + \frac{\cos^{(3)}0}{3!}x^3 + \frac{\cos^{(4)}0}{4!}x^4 +\cdots \cr &= 1 - \sin 0\cdot x - \frac{\cos 0}{2!}x^2 + \frac{\sin 0}{3!}x^3 + \frac{\cos 0}{4!}x^4 +\cdots \cr &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} +\cdots \cr &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k)!}x^{2k} \end{aligned} \tag{1}$ ダランベールの収束判定法により、 $\begin{aligned} \lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| &= \lim_{n\to\infty}\left|\frac{\frac{(-1)^{n+1}}{(2(n+1))!}x^{2(n+1)}}{\frac{(-1)^n}{(2n)!}x^{2n}}\right| \cr &= \lim_{n\to\infty}\left|-\frac{x^2}{_{(2n+2)}P_2}\right| \cr &= 0 \end{aligned} \tag{2}$ $(1),(2)$ より、 $\begin{aligned} \therefore \cos x &= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} +\cdots \cr &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k)!}x^{2k} \end{aligned}$

正弦関数のマクローリン展開の導出：

$\begin{aligned} \sin x &= \sum_{k=0}^\infty\frac{\sin^{(k)}0}{k!}x^k \cr &= \frac{\sin^{(0)} 0}{0!}x^0 + \frac{\sin^{(1)} 0}{1!}x^1 + \frac{\sin^{(2)}0}{2!}x^2 + \frac{\sin^{(3)}0}{3!}x^3 + \frac{\sin^{(4)}0}{4!}x^4 +\cdots \cr &= 0 + \cos 0\cdot x - \frac{\sin 0}{2!}x^2 - \frac{\cos 0}{3!}x^3 + \frac{\sin 0}{4!}x^4 + \cdots \cr &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} +\cdots \cr &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)!}x^{2k+1} \end{aligned} \tag{1}$ ダランベールの収束判定法により、 $\begin{aligned} \lim_{n\to\infty}\left|\frac{a_{n+1}}{a_n}\right| &= \lim_{n\to\infty}\left|\frac{\frac{(-1)^{n+1}}{(2(n+1)+1)!}x^{2(n+1)+1}}{\frac{(-1)^n}{(2n+1)!}x^{2n+1}}\right| \cr &= \lim_{n\to\infty}\left|-\frac{x^2}{_{(2n+3)}P_2}\right| \cr &= 0 \end{aligned} \tag{2}$ $(1),(2)$ より、 $\begin{aligned} \therefore \sin x &= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} +\cdots \cr &= \sum_{k=0}^\infty\frac{(-1)^k}{(2k+1)!}x^{2k+1} \end{aligned}$

関連記事

• 微分
• sinc関数
• 商の微分法則
• リーマン積分
• 対数導関数
• テイラー展開
• ダランベールの収束判定法