blue271828's misc :-)

双曲線

#幾何学

Contents

呼称

定義

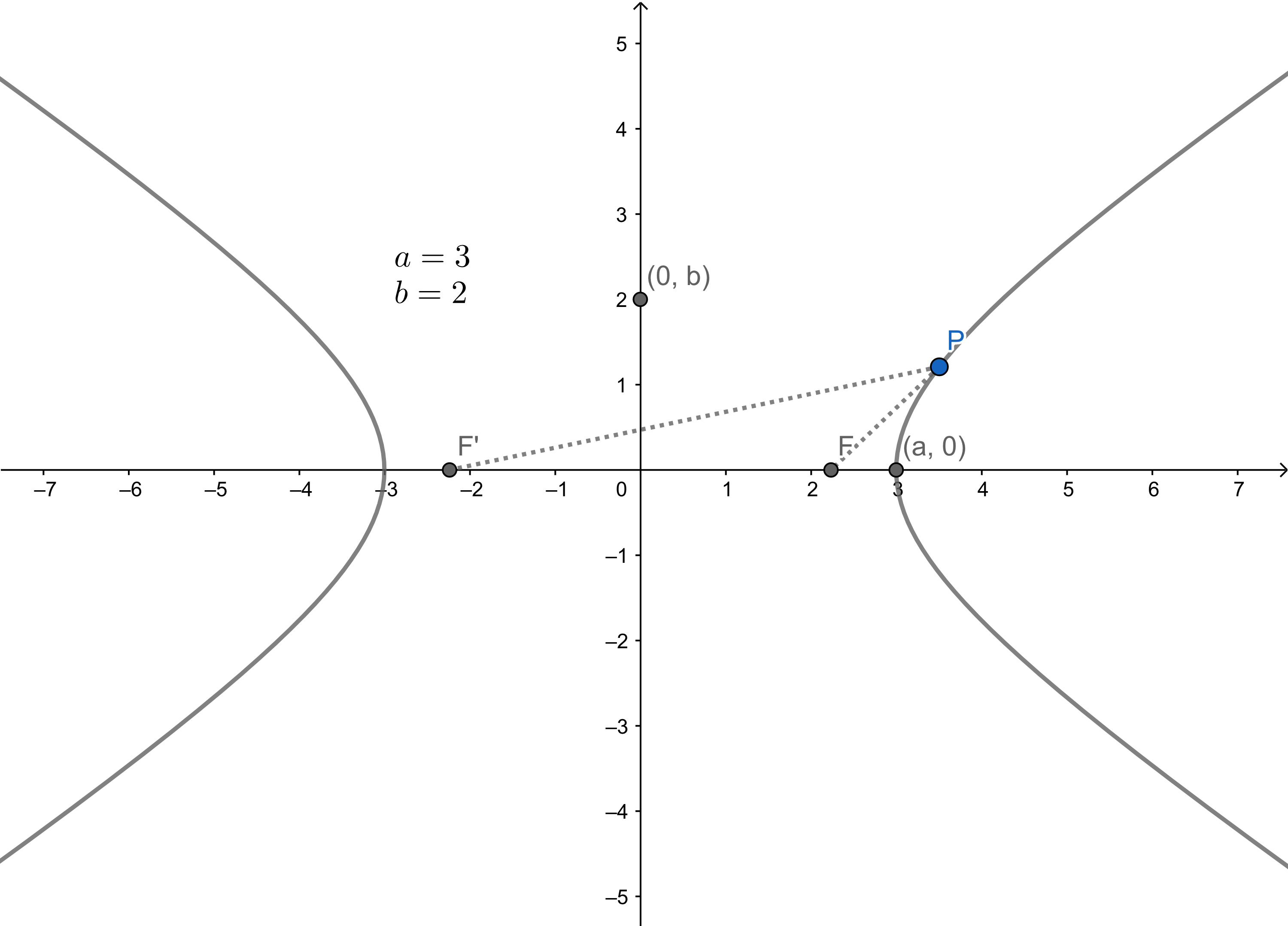
双曲線とは、二定点 F,F′F,F^\prime からの距離の 差 が一定である点 PP から作られる曲線である。点 F,F′F,F^\prime を焦点という。

双曲線の方程式 (標準形)

x2a2−y2b2=1(a>0, b>0) \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \quad (a>0,~b>0)

hyperbola

導出：

焦点 F,F′F,F^\prime の座標をそれぞれ、(c,0),(−c,0)(c,0),(-c,0) とする。

双曲線の定義から、∣FP−F′P∣=2a|FP-F^\prime P|=2a より、

∣(x+c)2+y2+(x−c)2+y2∣=2a(x+c)2+y2=±2a−(x−c)2+y2 \begin{aligned} \left|\sqrt{(x+c)^2+y^2}+\sqrt{(x-c)^2+y^2}\right| &= 2a \cr \sqrt{(x+c)^2+y^2} &= \pm{2a} - \sqrt{(x-c)^2+y^2} \end{aligned}

両辺を二乗して、整理する。

(x+c)2+y2=4a2±4a(x−c)2+y2+(x−c)2+y2±4a(x−c)2+y2=−4a2−(x−c)2+(x+c)2=−4a2−(x2−2cx+c2)+(x2+2cx+c2)=−4a2+4cx±a(x−c)+y2=−a2+cx \begin{aligned} (x+c)^2 + y^2 &= 4a^2 \pm 4a\sqrt{(x-c)^2+y^2} + (x-c)^2 + y^2 \cr \pm{4a\sqrt{(x-c)^2+y^2}} &= -4a^2 - (x-c)^2 + (x+c)^2 \cr &= -4a^2 - (x^2-2cx+c^2) + (x^2+2cx+c^2) \cr &= -4a^2 + 4cx \cr \pm{a\sqrt{(x-c)+y^2}} &= -a^2 + cx \end{aligned}

a2{(x−c)2+y2}=(−a2+cx)2a2(x2−2cx+c2+y2)=a4−2a2cx+c2x2a2x2−2a2cx+a2c2+a2y2=a4−2a2cx+c2x2a2x2+a2c2+a2y2=a4+c2x2a2x2−c2x2+a2y2=a4−a2c2(a2−c2)x2+a2y2=a2(a2−c2) \begin{aligned} a^2\{(x-c)^2+y^2\} &= (-a^2+cx)^2 \cr a^2(x^2-2cx+c^2+y^2) &= a^4 - 2a^2cx + c^2x^2 \cr a^2x^2-2a^2cx+a^2c^2+a^2y^2 &= a^4 - 2a^2cx + c^2x^2 \cr a^2x^2+a^2c^2+a^2y^2 &= a^4 + c^2x^2 \cr a^2x^2-c^2x^2+a^2y^2 &= a^4-a^2c^2 \cr (a^2-c^2)x^2 + a^2y^2 &= a^2(a^2-c^2) \end{aligned}

両辺を a2(a2−c2)a^2 (a^2 - c^2) で割ると、

x2a2−y2c2−a2=1 \frac{x^2}{a^2}-\frac{y^2}{c^2-a^2} = 1

bb は (0,b)(0,b) を BB , (a,0)(a,0) を AA としたとき、OF′=ABOF^\prime=AB となるような bb の値であることから、

b2=c2−a2 b^2 = c^2 - a^2

よって、

x2a2−y2b2=1 \frac{x^2}{a^2}-\frac{y^2}{b^2} = 1

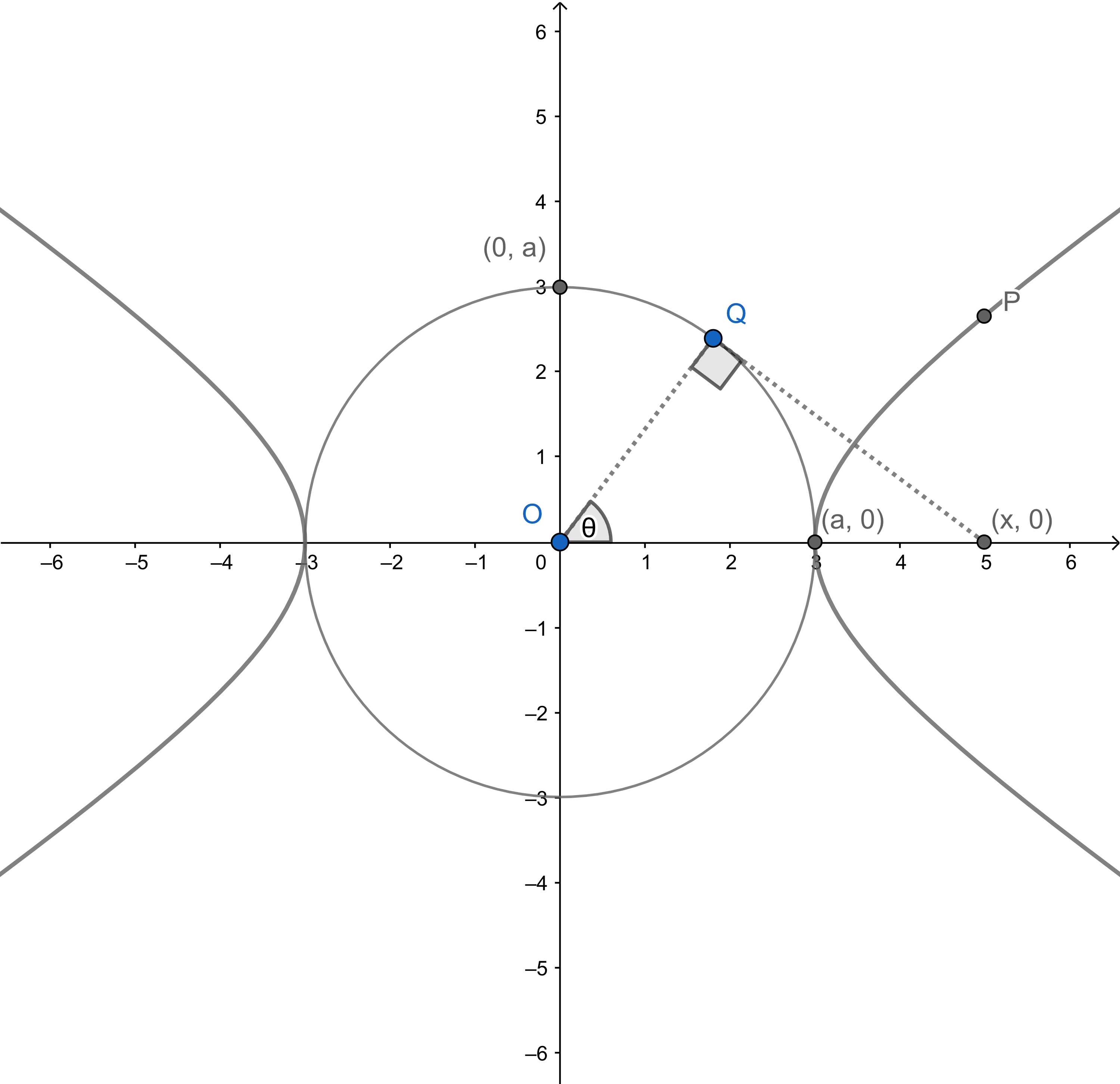
双曲線の媒介変数表示

{x=acos⁡θy=btan⁡θ \begin{cases} x &= \displaystyle\frac{a}{\cos{\theta}} \cr y &= b\tan{\theta} \end{cases}

parametric-representation

導出：

上図において ∠Q=90∘\angle{Q}=90^\circ を満たす θ\theta を媒介変数とする。これにより、

x=acos⁡θ x = \frac{a}{\cos{\theta}}

双曲線の標準形から、対応する yy を求める。

x2a2−y2b2=11a2⋅a2cos⁡2θ−y2b2=11cos⁡2θ=1+y2b2yb=tan⁡θy=btan⁡θ \begin{aligned} \frac{x^2}{a^2} - \frac{y^2}{b^2} &= 1 \cr \frac{1}{a^2}\cdot\frac{a^2}{\cos^2{\theta}} - \frac{y^2}{b^2} &= 1 \cr \frac{1}{\cos^2{\theta}} &= 1 + \frac{y^2}{b^2} \cr \frac{y}{b} &= \tan{\theta} \cr y &= b\tan{\theta} \end{aligned}

よって、

{x=acos⁡θy=btan⁡θ \begin{cases} x &= \displaystyle\frac{a}{\cos{\theta}} \cr y &= b\tan{\theta} \end{cases}

参考文献

Tags

#Ansible (3) #Bash (1) #Docker (1) #Git (2) #Hugo (2) #Molecule (1) #Python (1) #WSLtty (1) #アルゴリズム (4) #ビジネス用語 (1) #プログラミング (1) #位相空間論 (8) #初等数学 (20) #初等関数 (1) #実解析 (1) #幾何学 (3) #微分積分学 (18) #情報理論 (4) #抽象代数学 (14) #数理モデル (2) #数理論理学 (21) #機械学習 (3) #正規表現 (1) #測度論 (3) #特殊関数 (4) #確率論 (18) #組合せ論 (5) #統計学 (12) #線型代数学 (18) #複素解析学 (4) #解析学 (15) #論理学 (6) #順序集合論 (9)