blue271828's misc :-)

sinc関数

#初等数学

Contents

sinc関数

sinc関数 (英：sinc function) とは、正弦関数をその変数で割る関数のこと。sinc関数は、非正規化sinc関数と正規化sinc関数の二つの定義を持つ。当記事では、非正規化sinc関数をsinc関数の定義として取り扱う。

非正規化 sinc関数

数学では、非正規化sinc関数 (英：unnormalized sinc function) が定義として用いられる。

sinc⁡(x)=sin⁡xx(x≠0) \operatorname{sinc}(x) = \frac{\sin x}{x} \quad (x\ne 0)

正規化sinc関数

デジタル信号処理、情報理論では、正規化sinc関数 (英：normalized sinc function)が定義として用いられる。

sinc⁡(x)=sin⁡πxπx \operatorname{sinc}(x) = \frac{\sin\pi x}{\pi x}

sinc関数の微分

sinc⁡′(x)=1 \operatorname{sinc}^\prime(x) = 1


sinc関数の微分の導出：

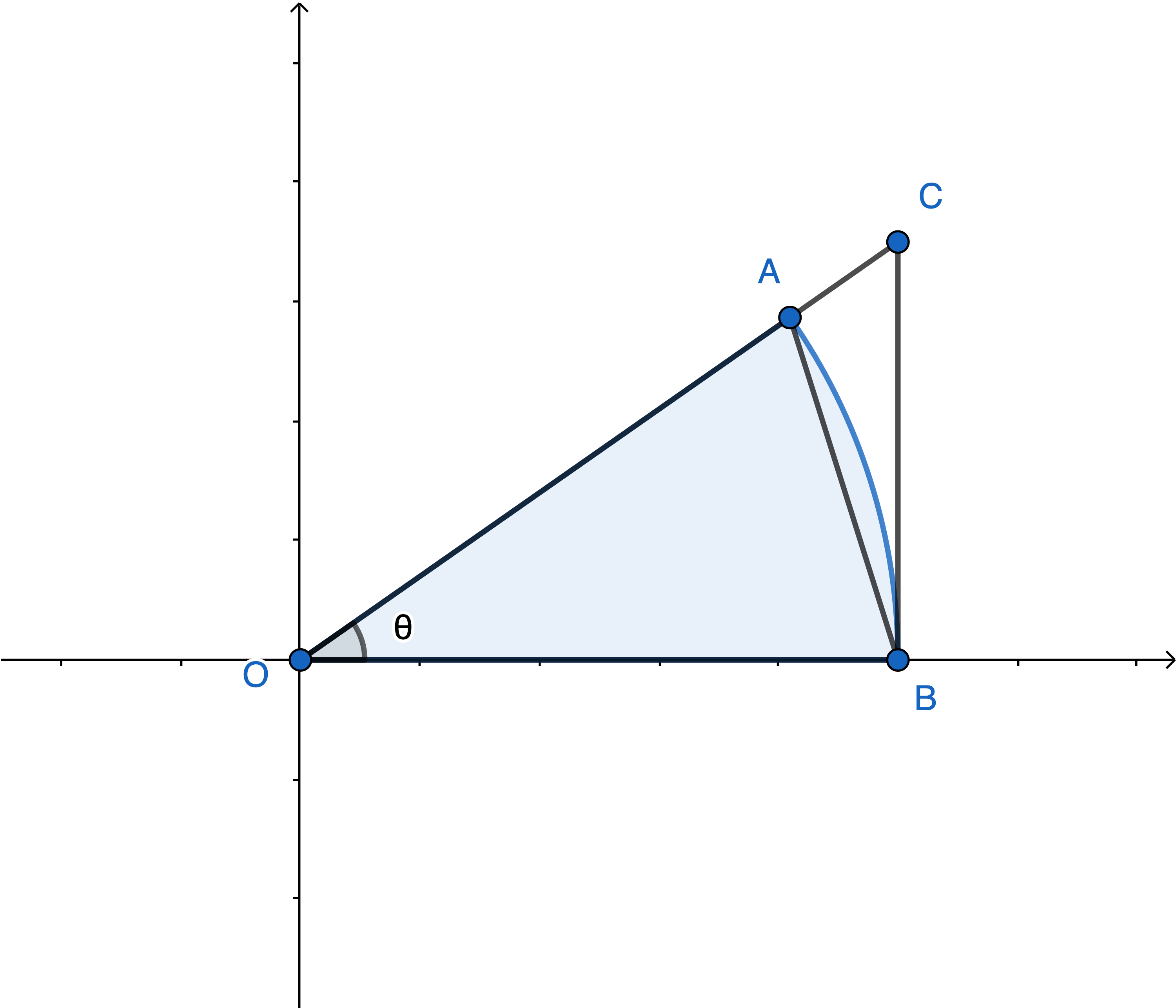
sinc-function

上図から次の関係が成り立つ。

△OAB<2π<△OBC=12sin⁡θ<12θ<12tan⁡θ \triangle{OAB}\lt 2\pi\lt\triangle{OBC} = \frac{1}{2}\sin\theta\lt\frac{1}{2}\theta\lt\frac{1}{2}\tan\theta

12sin⁡x\displaystyle \frac{1}{2}\sin x で割り、逆数をとると、

12sin⁡θ12tan⁡θ<12sin⁡θ12θ<12sin⁡θ12sin⁡θ=cos⁡θ<sin⁡θθ<1 \frac{\frac{1}{2}\sin\theta}{\frac{1}{2}\tan\theta}\lt \frac{\frac{1}{2}\sin\theta}{\frac{1}{2}\theta}\lt \frac{\frac{1}{2}\sin\theta}{\frac{1}{2}\sin\theta} = \cos\theta\lt\frac{\sin\theta}{\theta}\lt 1

ここで、x→0x\to 0 で極限をとると、

lim⁡θ→0cos⁡θ=1 \lim_{\theta\to 0} \cos\theta = 1

よってはさみうちの原理により、

lim⁡θ→0sin⁡θθ=1∴sinc⁡′x=1 \begin{aligned} \lim_{\theta\to 0}\frac{\sin\theta}{\theta} = 1 \cr \cr \therefore \operatorname{sinc}^\prime x = 1 \end{aligned}

関連記事

参考文献

Tags

#Ansible (3) #Bash (1) #Docker (1) #Git (2) #Hugo (2) #Molecule (1) #Python (1) #WSLtty (1) #アルゴリズム (4) #ビジネス用語 (1) #プログラミング (1) #位相空間論 (8) #初等数学 (20) #初等関数 (1) #実解析 (1) #幾何学 (3) #微分積分学 (18) #情報理論 (4) #抽象代数学 (14) #数理モデル (2) #数理論理学 (21) #機械学習 (3) #正規表現 (1) #測度論 (3) #特殊関数 (4) #確率論 (18) #組合せ論 (5) #統計学 (12) #線型代数学 (18) #複素解析学 (4) #解析学 (15) #論理学 (6) #順序集合論 (9)