逆三角関数
Contents
逆三角関数とは
逆三角関数 (英:inverse trigonometric function) とは、三角関数の逆関数のこと。三角関数は単写ではないため逆関数は定義域が制限される。
| 名称 | 定義 | 定義域 |
|---|---|---|
| 逆正弦関数 | $\arcsin(\sin x) = x$ | $-1\le x\le 1$ |
| 逆余弦関数 | $\arccos(\cos x) = x$ | $-1\le x\le 1$ |
| 逆正接関数 | $\arctan(\tan x) = x$ | $\forall{x}\in\R$ |
三角関数との関係
| $\theta$ | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|
| $\arcsin x$ | $\sin(\arcsin x) = x$ | $\cos(\arcsin x) = \sqrt{1-x^2}$ | $\displaystyle \tan(\arcsin x) = \frac{x}{\sqrt{1-x^2}}$ |
| $\arccos x$ | $\sin(\arccos x) = \sqrt{1-x^2}$ | $\cos(\arccos x) = x$ | $\displaystyle \tan(\arcsin x) = \frac{\sqrt{x^2-1}}{x}$ |
| $\arctan x$ | $\displaystyle \sin(\arctan x) = \frac{x}{\sqrt{1+x^2}}$ | $\displaystyle \cos(\arctan x) = \frac{1}{\sqrt{1+x^2}}$ | $\tan(\arctan x) = x$ |
三角関数との関係の導出:
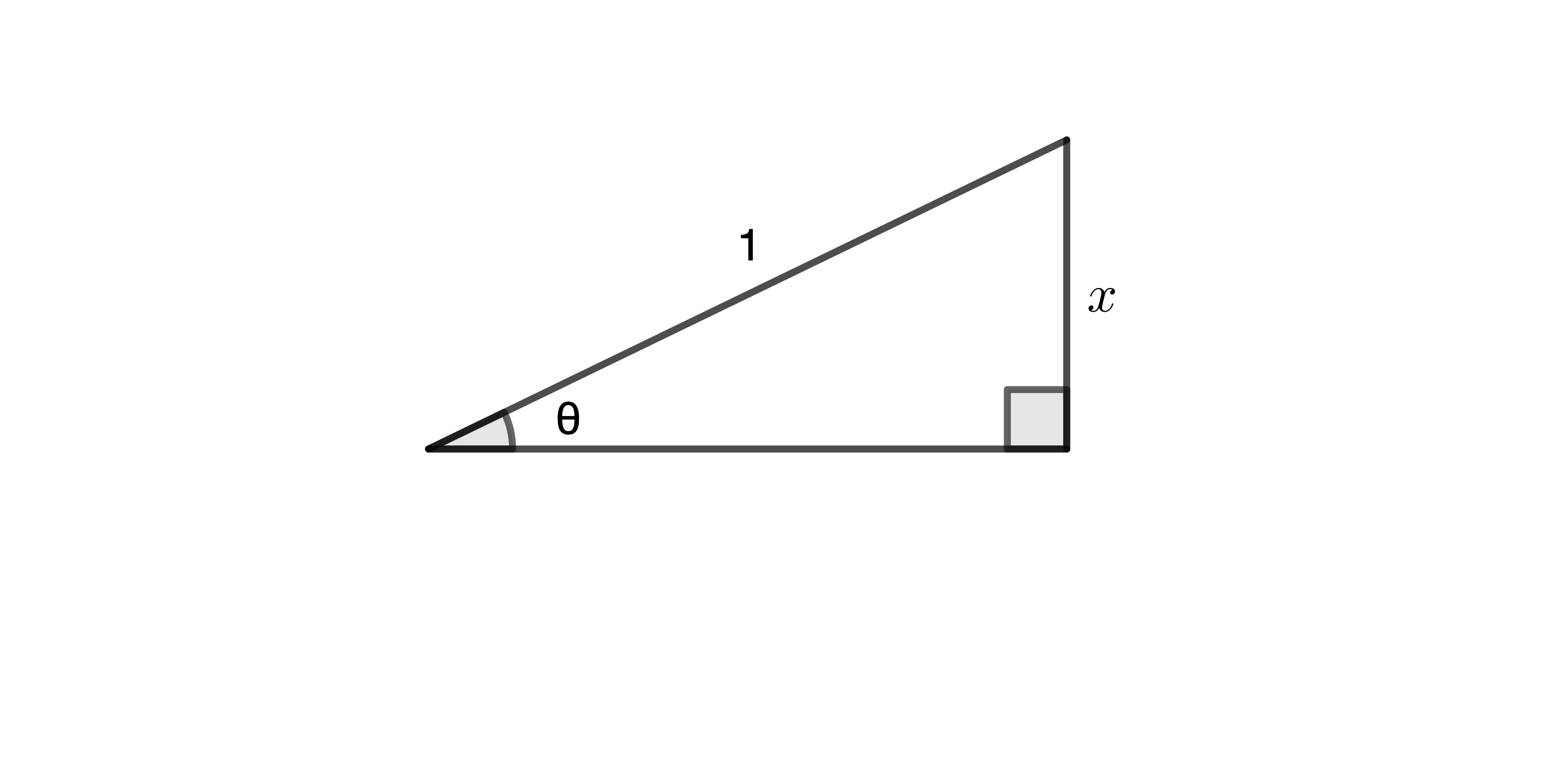
上図より、逆正弦関数と正弦関数の関係は、
\[ \begin{aligned} \sin\theta &= x \cr \arcsin x &= \theta \cr \cr \therefore \sin(\arcsin x) &= x \end{aligned} \tag{1} \]
ピタゴラスの定理により、
\[ \begin{aligned} 1 - x^2 &= \sqrt{1-x^2} \cr \cos\theta &= \sqrt{1-x^2} \cr \cr \therefore \cos(\arcsin x) &= \sqrt{1-x^2} \end{aligned} \tag{2} \]
$(1),(2)$ より、
\[ \begin{aligned} \tan(\arcsin x) &= \frac{\sin(\arcsin x)}{\cos(\arcsin x)} \cr &= \frac{x}{\sqrt{1-x^2}} \cr \cr \therefore \tan(\arcsin x) &= \frac{x}{\sqrt{1-x^2}} \end{aligned} \tag{3} \]
$(1),(2),(3)$ と同様に逆余弦関数・逆正接関数も求められる。
逆三角関数の微分
逆余弦関数の微分
\[ \arcsin^\prime x = \frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1 \]
逆余弦関数の微分の導出:
\[ \begin{aligned} f(x) &= \arcsin x, \quad -1\le x\le 1\cr x &= \sin f(x) \cr (x)^\prime &= (\sin f(x))^\prime \cr 1 &= \cos f(x) f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= \frac{1}{\cos f(x)} \cr &= \frac{1}{\cos(\arcsin x)} \cr &= \frac{1}{\sqrt{1-x^2}} \cr \cr \therefore \arcsin^\prime x &= \frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1\cr \end{aligned} \]
逆正弦関数の微分
\[ \arccos^\prime x = -\frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1 \]
逆正弦関数の微分の導出:
\[ \begin{aligned} f(x) &= \arccos x, \quad -1\le x\le 1 \cr x &= \cos f(x) \cr (x)^\prime &= (\cos f(x))^\prime \cr 1 &= -\sin f(x)f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= -\frac{1}{\sin f(x)} \cr &= -\frac{1}{\sin(\arccos x)} \cr &= -\frac{1}{\sqrt{1-x^2}} \cr \cr \therefore \arccos^\prime x &= -\frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1 \end{aligned} \]
逆正接関数の微分
\[ \arctan^\prime x = \frac{1}{1+x^2}, \quad x\in\R \]
逆正接関数の微分の導出:
\[ \begin{aligned} f(x) &= \arctan x, \quad x\in\R \cr x &= \tan f(x) \cr (x)^\prime &= (\tan f(x))^\prime \cr 1 &= \frac{1}{\cos^2 f(x)}f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= \cos^2 f(x) \cr &= \cos^2(\arctan x) \cr &= \frac{1}{1+x^2} \cr \cr \therefore \arctan^\prime x &= \frac{1}{1+x^2}, \quad x\in\R \end{aligned} \]