blue271828's misc :-)

逆三角関数

#初等数学

Contents

逆三角関数とは

逆三角関数 (英：inverse trigonometric function) とは、三角関数の逆関数のこと。三角関数は単写ではないため逆関数は定義域が制限される。

名称 定義 定義域
逆正弦関数 arcsin⁡(sin⁡x)=x\arcsin(\sin x) = x −1≤x≤1-1\le x\le 1
逆余弦関数 arccos⁡(cos⁡x)=x\arccos(\cos x) = x −1≤x≤1-1\le x\le 1
逆正接関数 arctan⁡(tan⁡x)=x\arctan(\tan x) = x ∀x∈R\forall{x}\in\R

三角関数との関係

θ\theta sin⁡θ\sin\theta cos⁡θ\cos\theta tan⁡θ\tan\theta
arcsin⁡x\arcsin x sin⁡(arcsin⁡x)=x\sin(\arcsin x) = x cos⁡(arcsin⁡x)=1−x2\cos(\arcsin x) = \sqrt{1-x^2} tan⁡(arcsin⁡x)=x1−x2\displaystyle \tan(\arcsin x) = \frac{x}{\sqrt{1-x^2}}
arccos⁡x\arccos x sin⁡(arccos⁡x)=1−x2\sin(\arccos x) = \sqrt{1-x^2} cos⁡(arccos⁡x)=x\cos(\arccos x) = x tan⁡(arcsin⁡x)=x2−1x\displaystyle \tan(\arcsin x) = \frac{\sqrt{x^2-1}}{x}
arctan⁡x\arctan x sin⁡(arctan⁡x)=x1+x2\displaystyle \sin(\arctan x) = \frac{x}{\sqrt{1+x^2}} cos⁡(arctan⁡x)=11+x2\displaystyle \cos(\arctan x) = \frac{1}{\sqrt{1+x^2}} tan⁡(arctan⁡x)=x\tan(\arctan x) = x

三角関数との関係の導出：

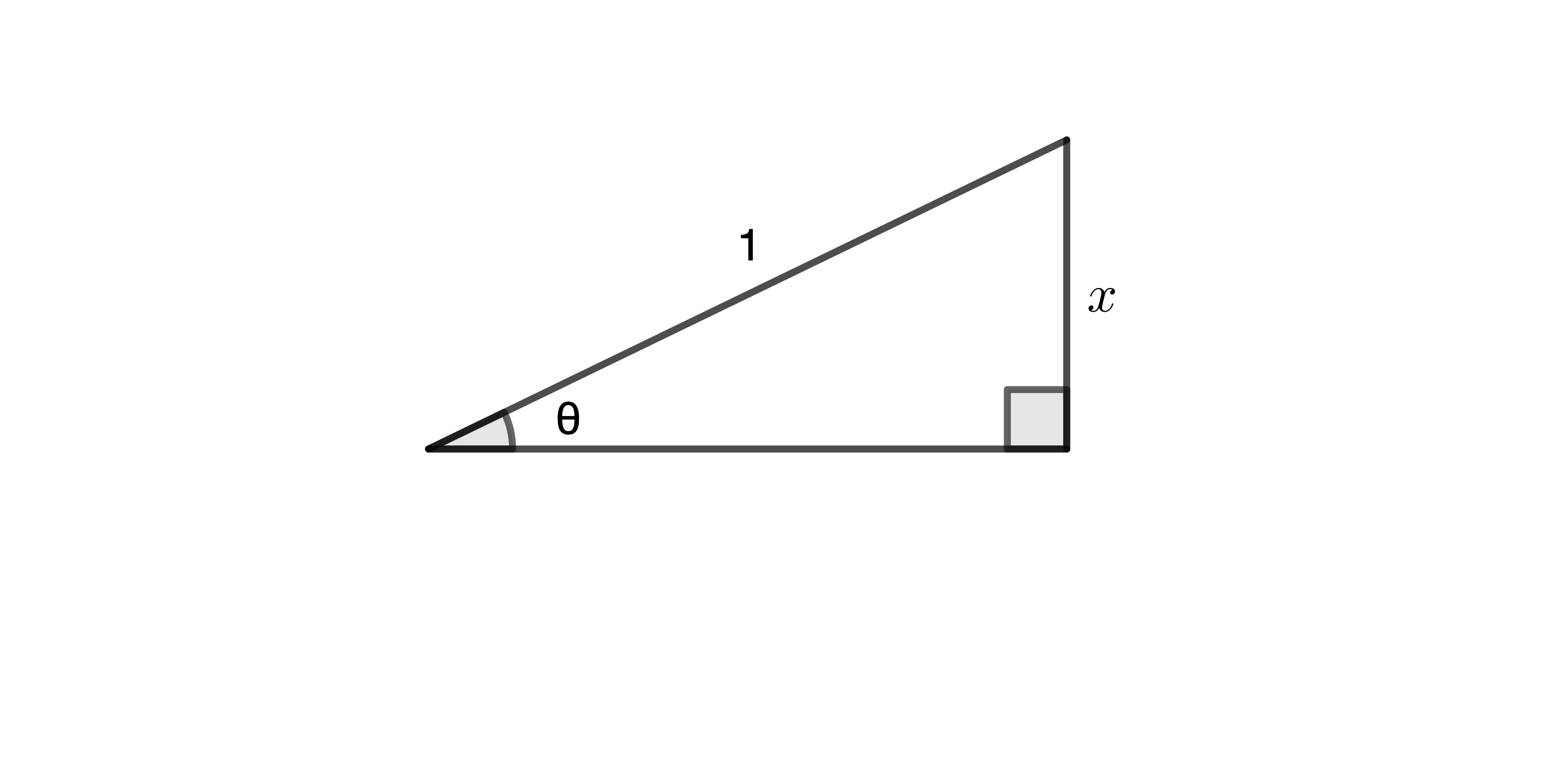
inverse-trigonometric-function

上図より、逆正弦関数と正弦関数の関係は、

sin⁡θ=xarcsin⁡x=θ∴sin⁡(arcsin⁡x)=x(1) \begin{aligned} \sin\theta &= x \cr \arcsin x &= \theta \cr \cr \therefore \sin(\arcsin x) &= x \end{aligned} \tag{1}

ピタゴラスの定理により、

1−x2=1−x2cos⁡θ=1−x2∴cos⁡(arcsin⁡x)=1−x2(2) \begin{aligned} 1 - x^2 &= \sqrt{1-x^2} \cr \cos\theta &= \sqrt{1-x^2} \cr \cr \therefore \cos(\arcsin x) &= \sqrt{1-x^2} \end{aligned} \tag{2}

(1),(2)(1),(2) より、

tan⁡(arcsin⁡x)=sin⁡(arcsin⁡x)cos⁡(arcsin⁡x)=x1−x2∴tan⁡(arcsin⁡x)=x1−x2(3) \begin{aligned} \tan(\arcsin x) &= \frac{\sin(\arcsin x)}{\cos(\arcsin x)} \cr &= \frac{x}{\sqrt{1-x^2}} \cr \cr \therefore \tan(\arcsin x) &= \frac{x}{\sqrt{1-x^2}} \end{aligned} \tag{3}

(1),(2),(3)(1),(2),(3) と同様に逆余弦関数・逆正接関数も求められる。

逆三角関数の微分

逆余弦関数の微分

arcsin⁡′x=11−x2,−1≤x≤1 \arcsin^\prime x = \frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1

逆余弦関数の微分の導出：

f(x)=arcsin⁡x,−1≤x≤1x=sin⁡f(x)(x)′=(sin⁡f(x))′1=cos⁡f(x)f′(x)∵f(g(x))′=f′(g(x))g′(x)f′(x)=1cos⁡f(x)=1cos⁡(arcsin⁡x)=11−x2∴arcsin⁡′x=11−x2,−1≤x≤1 \begin{aligned} f(x) &= \arcsin x, \quad -1\le x\le 1\cr x &= \sin f(x) \cr (x)^\prime &= (\sin f(x))^\prime \cr 1 &= \cos f(x) f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= \frac{1}{\cos f(x)} \cr &= \frac{1}{\cos(\arcsin x)} \cr &= \frac{1}{\sqrt{1-x^2}} \cr \cr \therefore \arcsin^\prime x &= \frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1\cr \end{aligned}

逆正弦関数の微分

arccos⁡′x=−11−x2,−1≤x≤1 \arccos^\prime x = -\frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1

逆正弦関数の微分の導出：

f(x)=arccos⁡x,−1≤x≤1x=cos⁡f(x)(x)′=(cos⁡f(x))′1=−sin⁡f(x)f′(x)∵f(g(x))′=f′(g(x))g′(x)f′(x)=−1sin⁡f(x)=−1sin⁡(arccos⁡x)=−11−x2∴arccos⁡′x=−11−x2,−1≤x≤1 \begin{aligned} f(x) &= \arccos x, \quad -1\le x\le 1 \cr x &= \cos f(x) \cr (x)^\prime &= (\cos f(x))^\prime \cr 1 &= -\sin f(x)f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= -\frac{1}{\sin f(x)} \cr &= -\frac{1}{\sin(\arccos x)} \cr &= -\frac{1}{\sqrt{1-x^2}} \cr \cr \therefore \arccos^\prime x &= -\frac{1}{\sqrt{1-x^2}}, \quad -1\le x\le 1 \end{aligned}

逆正接関数の微分

arctan⁡′x=11+x2,x∈R \arctan^\prime x = \frac{1}{1+x^2}, \quad x\in\R

逆正接関数の微分の導出：

f(x)=arctan⁡x,x∈Rx=tan⁡f(x)(x)′=(tan⁡f(x))′1=1cos⁡2f(x)f′(x)∵f(g(x))′=f′(g(x))g′(x)f′(x)=cos⁡2f(x)=cos⁡2(arctan⁡x)=11+x2∴arctan⁡′x=11+x2,x∈R \begin{aligned} f(x) &= \arctan x, \quad x\in\R \cr x &= \tan f(x) \cr (x)^\prime &= (\tan f(x))^\prime \cr 1 &= \frac{1}{\cos^2 f(x)}f^\prime(x) \quad \because f(g(x))^\prime =f^\prime(g(x))g^\prime(x) \cr f^\prime(x) &= \cos^2 f(x) \cr &= \cos^2(\arctan x) \cr &= \frac{1}{1+x^2} \cr \cr \therefore \arctan^\prime x &= \frac{1}{1+x^2}, \quad x\in\R \end{aligned}

関連記事

Tags

#Ansible (3) #Bash (1) #Docker (1) #Git (2) #Hugo (2) #Molecule (1) #Python (1) #WSLtty (1) #アルゴリズム (4) #ビジネス用語 (1) #プログラミング (1) #位相空間論 (8) #初等数学 (20) #初等関数 (1) #実解析 (1) #幾何学 (3) #微分積分学 (18) #情報理論 (4) #抽象代数学 (14) #数理モデル (2) #数理論理学 (21) #機械学習 (3) #正規表現 (1) #測度論 (3) #特殊関数 (4) #確率論 (18) #組合せ論 (5) #統計学 (12) #線型代数学 (18) #複素解析学 (4) #解析学 (15) #論理学 (6) #順序集合論 (9)