複素数
Contents
複素数とは
複素数 (英:complex number) とは、実数と虚数単位を用いて形式的に書かれた式を一種の数と見なしたもの。また、虚数単位 (英:imaginary unit) とは、$-1$ の平方根を表す数のことであり、一般に $i$ と書かれる。
\[ z = x+iy \quad (z\in\Complex,x,y\in\R) \\ \Updownarrow \\ z = \Re(z) + i\Im(z) \]
| 記号 | 意味 |
|---|---|
| $\Complex$ | 複素数全体の集合 |
| $i$ | 虚数単位 (英:imaginary unit) |
| $\Re(z)$ | 実部 (英:real part) |
| $\Im(z)$ | 虚部 (英:imaginary part) |
複素数の相等関係
\[ z_1=z_2 \\ \Updownarrow \\ x_1=x_2\land y_1=y_2 \quad (z_n=x_n+i y_n) \]
複素数の四則演算
複素数を $z_n = x_n+iy_n$ と表すとき、複素数の四則演算は以下のようになる。
\[ \begin{aligned} \text{加減算} &: z_1\pm z_2 = (x_1\pm x_2) + i(y_1\pm y_2) \vphantom{\int} \\ \text{乗算} &: z_1 z_2 = (x_1x_2-y_1y_2)+i(x_2y_1+x_1y_2) \vphantom{\int} \\ \text{除算} &: \frac{z_1}{z_2} = \frac{x_1x_2 + y_1y_2}{x_2^2 + y_2^2} + i\frac{x_2y_1 - x_1y_2}{x_2^2 + y_2^2} \\ \end{aligned} \]
加減算の公式の導出:
\[ \begin{aligned} z_1\pm z_2 &= (x_1+iy_1) \pm (x_2+iy_2) \\ &= (x_1+x_2) \pm i(y_1+y_2) \\ \cr \therefore z_1\pm z_2 &= (x_1\pm x_2) + i(y_1\pm y_2) \end{aligned} \]
乗算の公式の導出:
\[ \begin{aligned} z_1z_2 &= (x_1+iy_1)(x_2+iy_2) \\ &= x_1x_2+ix_1y_2+ix_2y_1-y_1y_2 \\ &= (x_1x_2-y_1y_2) + i(x_1b_y+x_2y_1) \\ \\ \therefore z_1 z_2 &= (x_1x_2-y_1y_2)+i(x_2y_1+x_1y_2) \end{aligned} \]
除算の公式の導出:
\[ \begin{aligned} \displaystyle \frac{z_1}{z_2} &= \frac{x_1+iy_1}{x_2+iy_2} \cr &= \frac{(x_1+iy_1)(x_2-iy_2)}{(x_2+iy_2)(x_2-iy_2)} \cr &= \frac{x_1x_2+y_1y_2+ix_2y_1+ix_1y_2}{x_2^2+y_2^2} \cr &= \frac{x_1x_2+y_1y_2}{x_2^2+y_2^2} + i\frac{x_2y_1-x_1y_2}{x_2^2+y_2^2} \cr \cr \therefore \frac{z_1}{z_2} &= \frac{x_1x_2+y_1y_2}{x_2^2+y_2^2} + i\frac{x_2y_1-x_1y_2}{x_2^2+y_2^2} \end{aligned} \]
複素数の絶対値
複素数 $z=x+iy$ の絶対値は次式のように定義される。
\[ |z| = \sqrt{x^2+y^2} \]
複素数平面
複素数平面 (英:complex plane) とは、複素数 $x+yi$ を $xy$ 平面上の点 $(x,y)$ に対応させて表したもの。複素数平面はガウス平面 (英:Gaussian plane) とも呼ばれる。
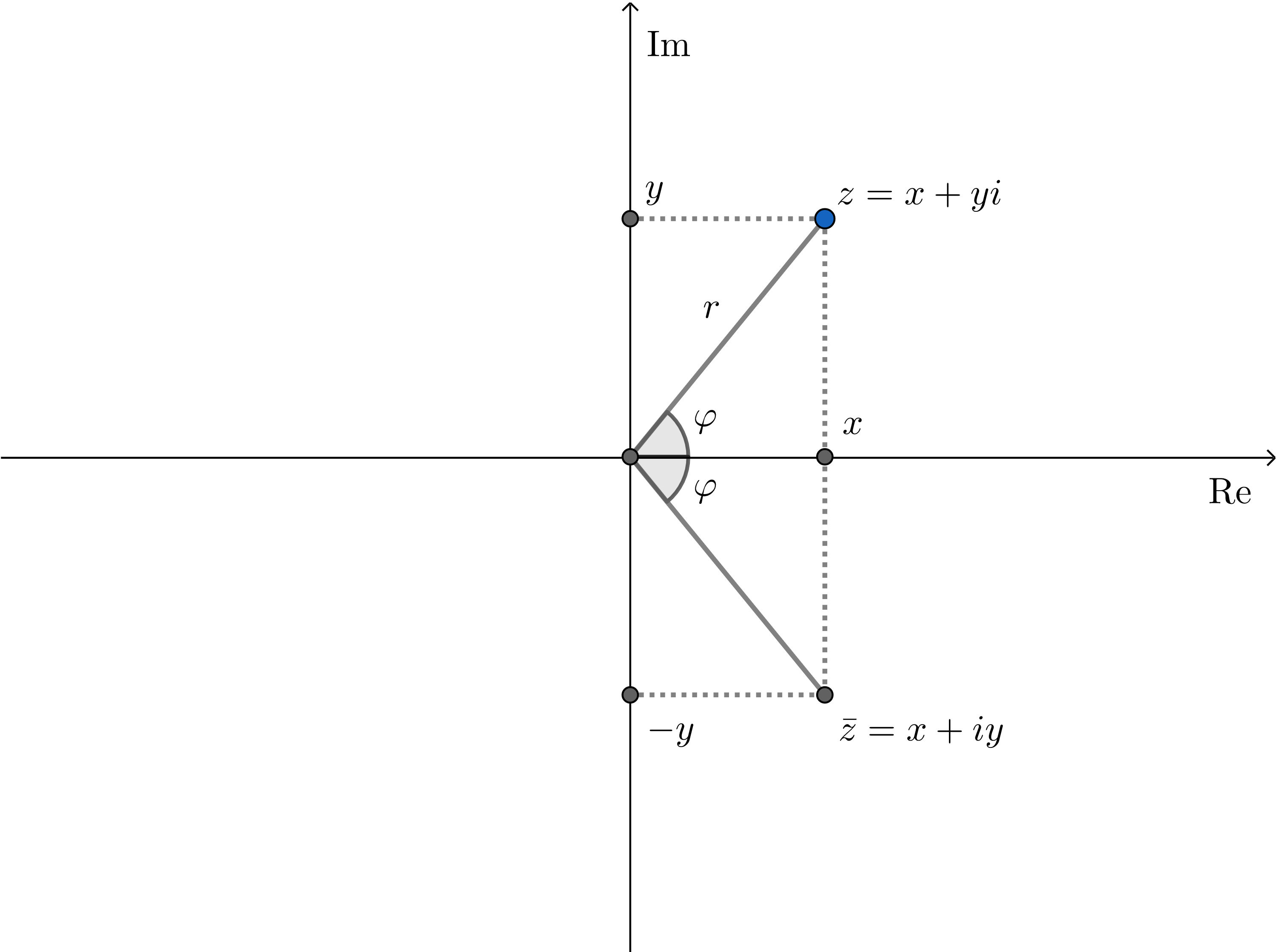
偏角
偏角 (英:argument) とは、複素数上の関数で $\arg(z)$ と書かれる。複素数平面の正の実軸から複素数 $z=x+yi$ を表すベクトルまでのラジアン $\varphi$ を与える。
極座標
極座標 (英:polar coordinates) とは、複素数平面上の点を、複素数 $z$ の絶対値 $r$ と偏角 $\theta$ の組 $(r,\theta)$ で表したもの。
極形式
極形式 (英:polar form) とは、複素数 $z$ を複素数 $z$ の絶対値 $r$ と偏角 $\theta$ を用いて表した形のこと。 \( z = r(\cos\theta+i\sin\theta) \quad \left(r=|z|,\tan\theta=\frac y x\right) \)
また極形式は、オイラーの公式を用いて以下のようにも表せる。
\[ r(\cos\theta + i\sin\theta) = re^{i\theta} \]
極形式を使った演算
\[ \begin{aligned} \text{乗算} &: z_1 z_2 = r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)) \vphantom{\int} \\ \text{除算} &: \frac{z_1}{z_2} = \frac{r_1}{r_2}(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)) \\ \end{aligned} \]
極形式を使った乗算の導出:
\[ \begin{aligned} z_1z_2 &= r_1(\cos\theta_1+i\sin\theta_1)r_2(\cos\theta_2+i\sin\theta_2) \\ &= r_1r_2(\cos\theta_1\cos\theta_2-\sin\theta_1\sin\theta_2 + i(\sin\theta_1\cos\theta_2+\cos\theta_1\sin\theta_2)) \\ &= r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)) \\ \\ \therefore z_1 z_2 &= r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2)) \\ \end{aligned} \]
極形式を使った除算の導出:
\[ \begin{aligned} \frac{z_1}{z_2} &= \frac{r_1(\cos\theta_1+i\sin\theta_1)}{r_2(\cos\theta_2+i\sin\theta_2)} \\ &= \frac{r_1(\cos\theta_2-i\sin\theta_2)(\cos\theta_1+i\sin\theta_1)}{r_2(\cos\theta_2-\sin\theta_2)(\cos\theta_2+i\sin\theta_2)} \\ &= \frac{r_1(\cos\theta_1\cos_2+\sin\theta_1\sin\theta_2+i(\sin\theta_1\cos\theta_2-\cos\theta_1\sin\theta_2))}{r_2} \\ &= \frac{r_1}{r_2}(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)) \\ \\ \therefore \frac{z_1}{z_2} &= \frac{r_1}{r_2}(\cos(\theta_1-\theta_2)+i\sin(\theta_1-\theta_2)) \end{aligned} \]