blue271828's misc :-)

双曲線関数

#初等関数 #特殊関数

Contents

双曲線関数とは

双曲線関数 (英：hyperbolic function) とは、単位円に対応する双曲線に関わる次図面積を θ2\displaystyle \frac{\theta}{2} とした際の各関数を指す。なお次図の場合、x=cosh⁡θ, y=sinh⁡θx=\cosh \theta, ~y=\sinh \theta で定義される。

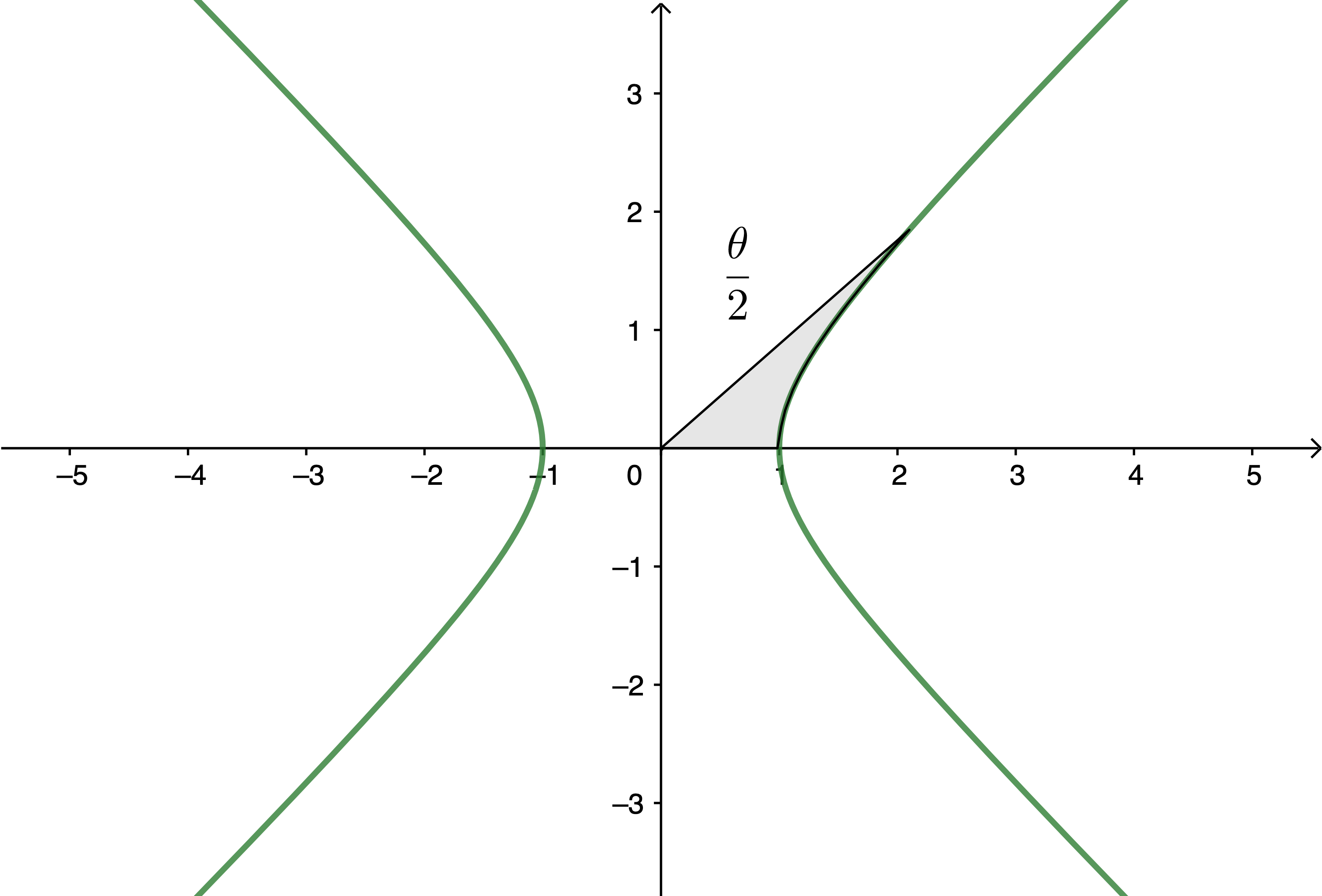
hyperbolic-function

双曲線余弦関数

cosh⁡θ=eθ+e−θ2 \cosh\theta = \frac{e^\theta+e^{-\theta}}{2}


双曲線余弦関数の導出：

上図より、

θ2=xx2−12−∫1xt2−1dt∵x2−y2=1(1) \frac{\theta}{2} = \frac{x\sqrt{x^2-1}}{2} - \int_1^x\sqrt{t^2-1}dt \quad \because x^2-y^2=1 \tag{1}

右項の不定積分を FF とすると、

F(t)=∫t2−1dt=∫(t)′t2−1dt=tt2−1−∫t(t2−1)′dt=tt2−1−∫t2t2−1dt=tt2−1−∫(t2−1)+1t2−1dt=tt2−1−∫t2−1dt−∫1t2−1dt=tt2−1−F(t)−ln⁡∣t+t2−1∣+C2F(t)=tt2−1−ln⁡∣t+t2−1∣+CF(t)=12(tt2−1−ln⁡∣t+t2−1∣+C)(2) \begin{aligned} F(t) &= \int\sqrt{t^2-1}dt \cr &= \int(t)^\prime\sqrt{t^2-1}dt \cr &= t\sqrt{t^2-1} - \int{t\left(\sqrt{t^2-1}\right)^\prime dt} \cr &= t\sqrt{t^2-1} - \int{\frac{t^2}{\sqrt{t^2-1}} dt} \cr &= t\sqrt{t^2-1} - \int{\frac{(t^2-1)+1}{\sqrt{t^2-1}} dt} \cr &= t\sqrt{t^2-1} - \int{\sqrt{t^2-1}dt} - \int{\frac{1}{\sqrt{t^2-1}} dt} \cr &= t\sqrt{t^2-1} - F(t) - \ln\left|t+\sqrt{t^2-1}\right| + C \cr 2F(t) &= t\sqrt{t^2-1} - \ln\left|t+\sqrt{t^2-1}\right| + C \cr F(t) &= \frac{1}{2}\left(t\sqrt{t^2-1}-\ln\left|t+\sqrt{t^2-1}\right| + C\right) \end{aligned} \tag{2}

(1),(2)(1),(2) から、

θ2=xx2−12−∫1xt2−1dt=xx2−12−F(x)+F(1)=xx2−12−12(xx2−1−ln⁡∣x+x2−1∣)=12ln⁡∣x+x2−1∣θ=ln⁡∣x+x2−1∣eθ=x+x2−1(3) \begin{aligned} \frac{\theta}{2} &= \frac{x\sqrt{x^2-1} }{2} - \int_1^x\sqrt{t^2-1}dt \cr &= \frac{x\sqrt{x^2-1} }{2} - F(x) + F(1) \cr &= \frac{x\sqrt{x^2-1} }{2} - \frac{1}{2}\left(x\sqrt{x^2-1}-\ln\left|x+\sqrt{x^2-1}\right|\right) \cr &= \frac{1}{2}\ln\left|x+\sqrt{x^2-1}\right| \cr \theta &= \ln\left|x+\sqrt{x^2-1}\right| \cr e^\theta &= x+\sqrt{x^2-1} \end{aligned} \tag{3}

(3)(3) から、e−θe^{-\theta} を得る。

e−θ=1x+x2−1=x−x2−1(x+x2−1)(x−x2−1)=x−x2−1(4) \begin{aligned} e^{-\theta} &= \frac{1}{x+\sqrt{x^2-1}} \cr &= \frac{x-\sqrt{x^2-1}}{\left(x+\sqrt{x^2-1}\right)\left(x-\sqrt{x^2-1}\right)} \cr &= x-\sqrt{x^2-1} \end{aligned} \tag{4}

(3),(4)(3),(4) より、

eθ+e−θ=2xx=eθ+e−θ2∴cosh⁡θ=eθ+e−θ2 \begin{aligned} e^\theta + e^{-\theta} &= 2x \cr x &= \frac{e^\theta+e^{-\theta}}{2} \cr \cr \therefore \cosh\theta = \frac{e^\theta+e^{-\theta}}{2} \end{aligned}

双曲線正弦関数

sinh⁡θ=eθ−e−θ2 \sinh\theta = \frac{e^\theta-e^{-\theta}}{2}


双曲線正弦関数の導出：

双曲線余弦関数の導出から、

eθ−e−θ=2x2−1=2y∵x2−y2=1y=eθ−e−θ2∴sinh⁡θ=eθ−e−θ2 \begin{aligned} e^\theta - e^{-\theta} &= 2\sqrt{x^2-1} \cr &= 2y \quad \because x^2-y^2=1 \cr y &= \frac{e^\theta-e^{-\theta}}{2} \cr \cr \therefore \sinh\theta &= \frac{e^\theta-e^{-\theta}}{2} \end{aligned}

関連記事

Tags

#Ansible (3) #Bash (1) #Docker (1) #Git (2) #Hugo (2) #Molecule (1) #Python (1) #WSLtty (1) #アルゴリズム (4) #ビジネス用語 (1) #プログラミング (1) #位相空間論 (8) #初等数学 (20) #初等関数 (1) #実解析 (1) #幾何学 (3) #微分積分学 (18) #情報理論 (4) #抽象代数学 (14) #数理モデル (2) #数理論理学 (21) #機械学習 (3) #正規表現 (1) #測度論 (3) #特殊関数 (4) #確率論 (18) #組合せ論 (5) #統計学 (12) #線型代数学 (18) #複素解析学 (4) #解析学 (15) #論理学 (6) #順序集合論 (9)