ラグランジュの平均値の定理
ラグランジュの平均値の定理 (Lagrange’s mean value theorem) とは、函数 f(x) が、閉区間 [a,b] において連続かつ、開区間 (a,b) において微分可能なとき、線 AB と平行な接線をもつ点が a と b の間に存在するという主張。
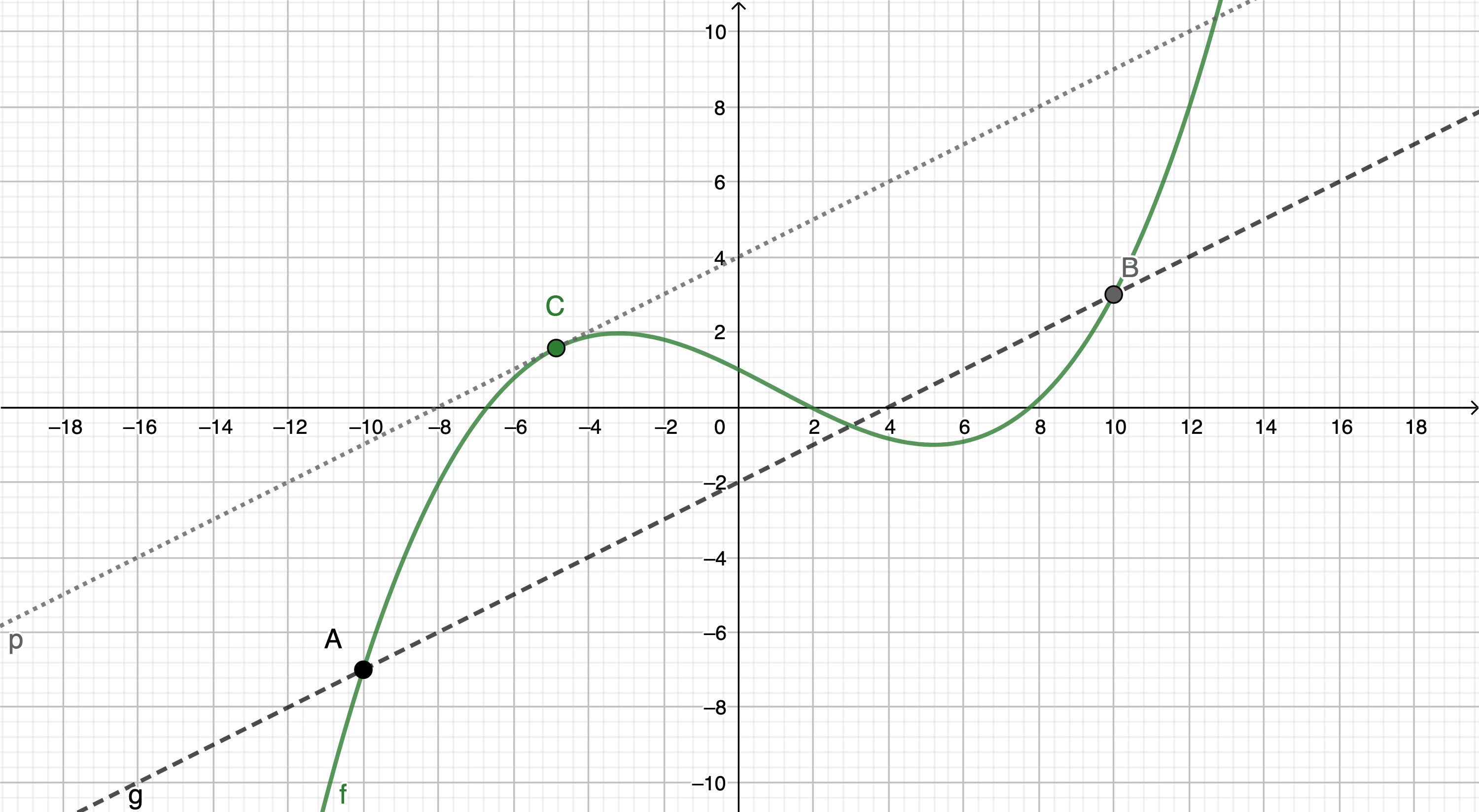
ラグランジュの平均値の定理:
a<b とし、f(x) を閉区間 [a,b] で連続で、開区間 (a,b) で微分可能な函数とする。このとき開区間 (a,b) 上にある点 c が存在して、
b−af(b)−f(a)=f′(c)
が成り立つ。
ラグランジュの平均値の定理の証明:
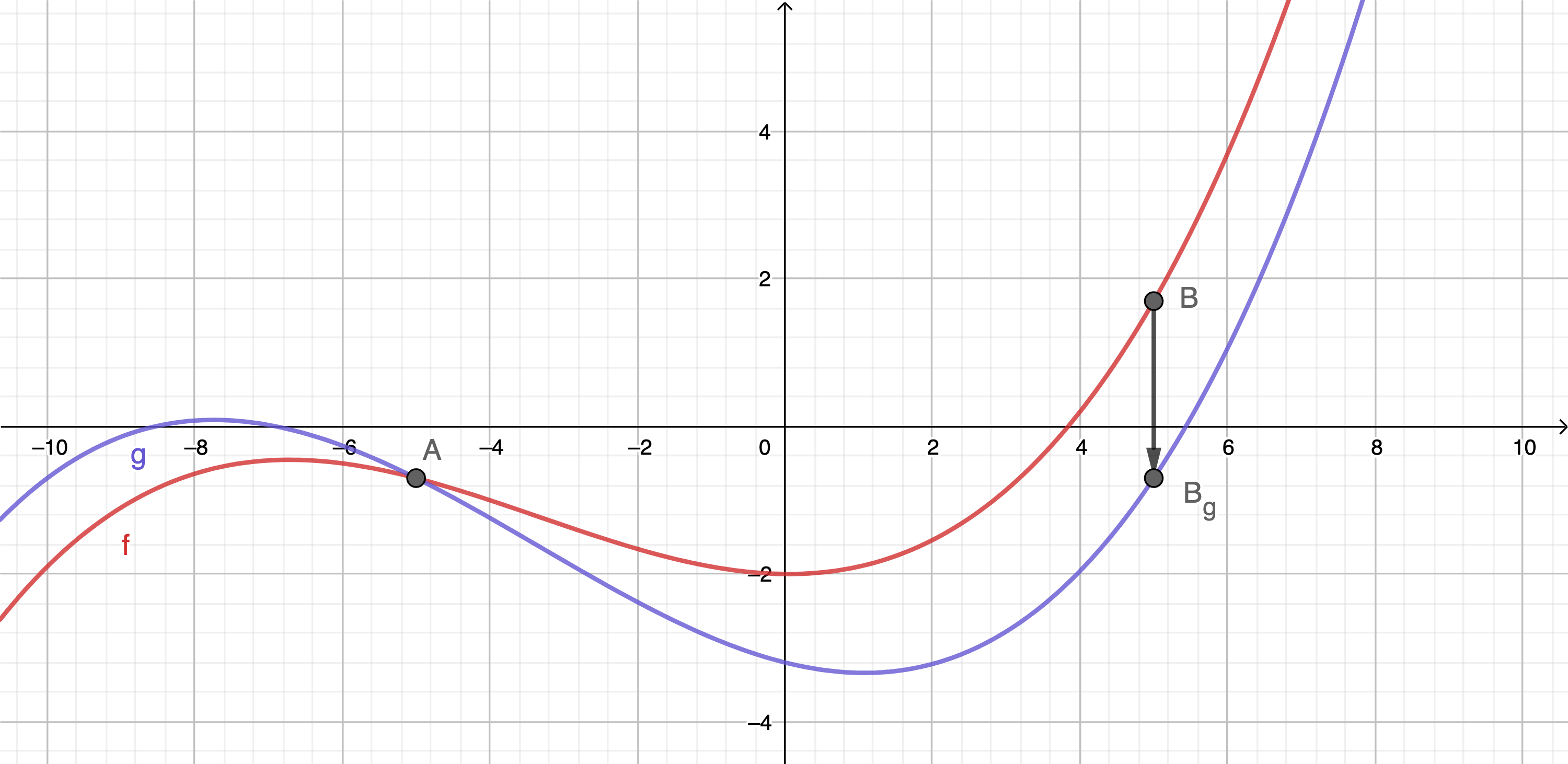
g(x)=f(x)−b−af(b)−f(a)(x−a)
とする。g(x) は、閉区間 [a,b] において連続かつ、開区間 (a,b) において微分可能な函数であり、
g(a)g(b)=f(a)−b−af(a)−f(a)(a−a)=f(a)=f(b)−b−af(b)−f(a)(b−a)=f(a)
より、g(a)=g(b) である。
これにより g(x) はロルの定理の条件を満たすため、g′(c)=0, a<c<b を満たす c は存在する。また、
g′(x)=[f(x)−b−af(b)−f(a)(x−a)]′=[f(x)−b−af(b)−f(a)x+b−af(b)−f(a)a]′=f′(x)−b−af(b)−f(a)
により、x=c における f′(c) は、
g′(x)f′(c)=f′(c)−b−af(b)−f(a)=0=b−af(b)−f(a)
である。よって閉区間 [a,b] で連続で、開区間 (a,b) で微分可能な函数 f(x) には、開区間 (a,b) 上に、
b−af(b)−f(a)=f′(c)
を満たす点 c が存在する。
参考文献

